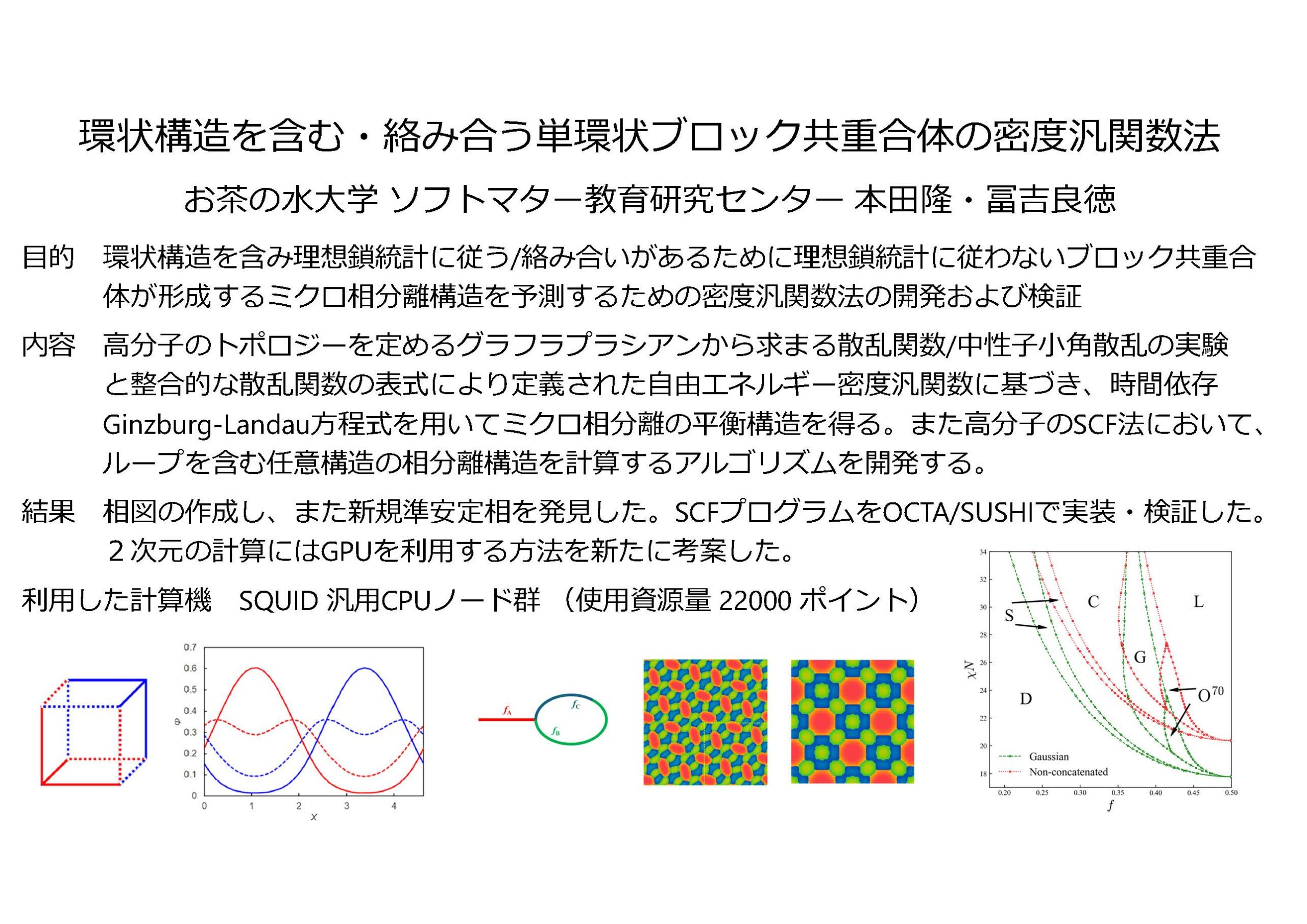
環状構造を含む・絡み合う単環状ブロック共重合体の密度汎関数法
氏名:冨吉良徳、本田隆
所属:お茶の水女子大学 ソフトマター教育研究センター
概要:環状構造を含む一般的なトポロジー構造を持つブロック共重合体のミクロ相分離構造を予測する方法論は確立されていなかった。また絡み合いを持つ単環状ブロック共重合体の相挙動は、理想鎖統計に従わないために従来の方法論では予測することが出来ない。上記の問題を克服するため、理想鎖統計に従う任意のトポロジー構造を持つ/絡み合い持つ単環状ブロック共重合体の密度汎関数法(自己無撞着場理論・Ginzburg-Landau理論)を開発した。グラフ理論や中性子実験の知見を用いてそれぞれの理論を発展させシミュレーションを行うことで、対象とした系の相図や新規の準安定相を明らかにした。
論文掲載,発表実績:
(学術雑誌掲載論文)
- Yoshinori Tomiyoshi, Takashi Honda, Toshihiro Kawakatsu, Takahiro Murashima, Erica Uehara, Tetsuo Deguchi, "Density Functional Theory for Cyclic Block Copolymer Melts", Macromolecules, Vol.57, no.22, p.10704-10716, Nov. 2024
(その他)
- 本田隆・冨吉良徳・川勝年洋, "ループ構造を含むポリマーの自己無撞着場理論", 第73回高分子討論会, 新潟大学五十嵐キャンパス, 2024年9月26日
- 冨吉良徳・本田隆・川勝年洋, "絡み目をもたない環状ブロック共重合体のミクロ相分離の密度汎関数法", 第73回高分子討論会, 新潟大学五十嵐キャンパス, 2024年9月26日
Posted : 2025年03月31日