所属：理化学研究所計算科学研究センター

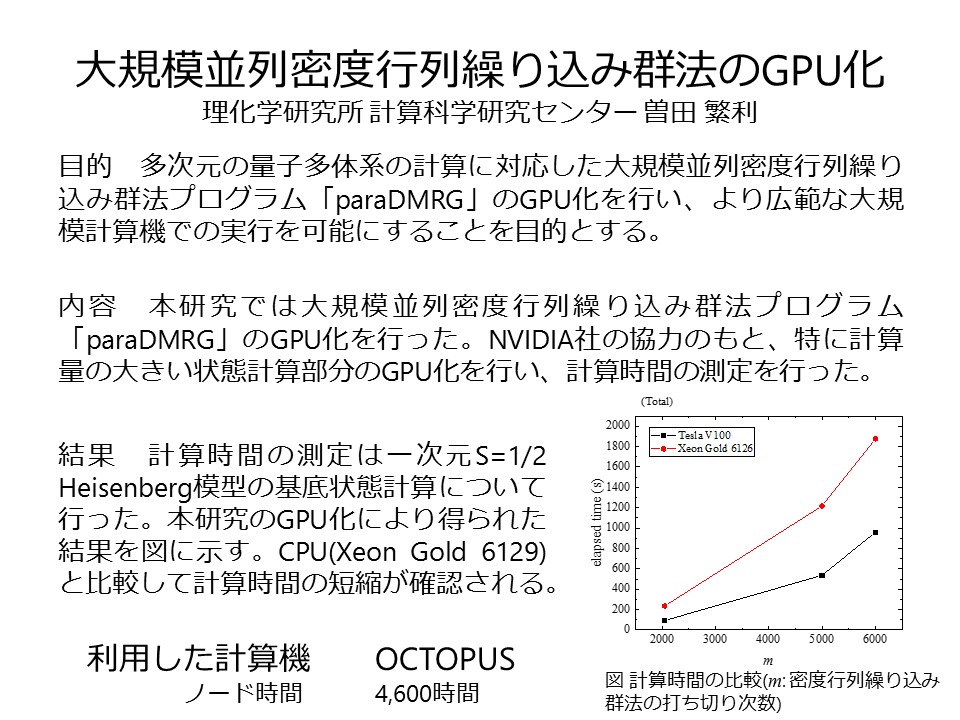
概要：密度行列繰り込み群法は強相関量子系に対する数値的研究手法であり、特に１次元系に対して有効な手法であることが知られている。その一方、密度行列繰り込み群法の多次元系に対する高精度計算は、その量子揺らぎのため非常に巨大な計算コストを要することが知られており、この事情はエンタングルメント・エントロピーの面積則と対応する。しかしながら、近年の計算機科学の発展は密度行列繰り込み群法の2次元系への応用を十分可能にしており、数多くの研究成果も報告されている。密度行列繰り込み群法の２次元系への応用は、例えば量子モンテカルロ法ではいわゆる負符号問題のために適用することが困難な系に対しても適用可能であり、量子スピン液体状態のような新奇量子相の研究など様々な応用も期待される。本研究では、これまで開発してきた大規模並列密度行列繰り込み群法プログラム「paraDMRG」のGPU化を行うことにより、GPUが搭載されている大規模計算機での効率的な実行を可能にすることで、より広範な応用を促進することを目的とする。

論文掲載,発表実績:
（学術雑誌掲載論文）

• S Ohmura, A Takahashi, K Iwano, T Yamaguchi, K Shinjo, T Tohyama, S Sota, H Okamoto, “Effective model of one-dimensional extended Hubbard systems: Application to linear optical spectrum calculations in large systems based on many-body Wannier functions”, Physical Review B 100 (23), 235134 (2019).

（国際会議会議録掲載論文）

• S. Sota, T. Shirakawa, S. Yunoki, T. Tohyama , “Dynamical DMRG Study of Spin Excitation Dynamics on the Triangular Lattice Antiferromagnetic Heisenberg model”, International Conference on Strongly Correlated Electron Systems 2019, 2019/9, Okayama.
• S. Sota, “Quantum dynamics simulation towards Fugaku”, The 2nd International Symposium, 2020/2, Kobe.
• S. Sota, T. Shirakawa, S. Yunoki, T. Tohyama, “Dynamical DMRG study of spin excitation dynamics in triangular lattice spin-1/2 antiferromagnet”, APS March Meeting 2020, 2020/3, Denver (USA).
• K. Shinjo, S. Sota, S. Yunoki, T. Tohyama, “Characterization of photoexcited states in the half-filled one-dimensional extended Hubbard model assisted by machine learning”, APS March Meeting 2020, 2020/3, Denver (USA).
• B. H. Kim, S. Sota, T. Shirakawa, Y. Son, S. Yunoki, “Intermediate magnetic phase of the proximate Kitaev system in the in-plane magnetic field”, APS March Meeting 2020, 2020/3, Denver (USA).